How To Find The X Intercept In Vertex Form

The difficulty of graphing a quadratic role varies depending on the class yous notice information technology in. We'll start things off relatively easily.

f(x) = a(10 – h)² + k

No, nosotros're not lying to y'all; that is a quadratic office. Go ahead, multiply information technology out.

f(x) = ax ^two + (-twoah)ten + (ah ^two + k)

The h and thou are constants, so (-2ah) and (ah ² + k) are also constants, which nosotros could phone call, say, b and c. See, y'all can trust usa, it's totally quadratic.

When you take a parabola written out like f(10) = a(ten – h)² + chiliad, information technology'southward in vertex class. With vertex grade, you take several pieces of important data thrown at you correct away. When you get-go run into someone, your starting time impression tends to stick with you. Information technology's the same with this equation.

The sign of a tells you if the parabola opens up or down. If a is positive, information technology opens up. If a is being a Negative Nancy, the parabola opens downwards. You also know that the vertex of the parabola is at the point (h, yard). Be careful with the sign of h, though.

Sample Problem

Graph the role f(x) = (x – 2)^two – 1.

The vertex of the parabola is at (h, m) = (2, –i). We can as well see that the parabola opens upwardly. We need a few more points, withal. We could make a table and start plugging in values of x, but there's unremarkably an easier way: find the intercepts of y and x (if they be). Starting with the y-intercept, which occurs at x = 0.

f(0) = (0 – ii)² – ane = 4 – one = iii

Right on: (0, 3) is a bespeak on our parabola. Now get for the ten-intercepts, which occur when y = 0, if there are any.

0 = (x – ii)² – 1

0 = x ^two – 4x + 4 – i

0 = x ² – 410 + 3

This quadratic equation can be factored.

0 = (x – three)(x – 1)

Then, (1, 0) and (3, 0) are also points on the parabola. Putting information technology all together gets us:

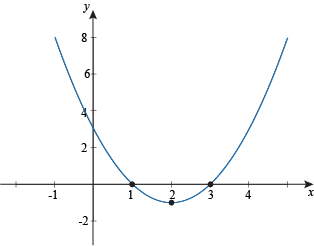
Run across? Math smarter, non harder.

Sample Problem

Graph the function f(x) = -2(ten + 1)² – 2.

We immediately see that the vertex is at (-ane, -2), and the parabola opens downward. Time to track downwardly our y-intercept.

f(0) = -2(0 + ane)ⁱⁱ – 2 = -2(1) – 2 = -four

Sweetness. The y-intercept is (0, -iv). At present nosotros hunt for the x-intercepts. Some say the use of dynamite while hunting is unsportsmanlike. They're probably right.

0 = -2(10 + i)² – two

0 = -2(x ² + iix + 1) – 2

0 = -twox ² – fourx – 2 – ii

0 = -iiten ^two – 4x – iv

0 = -ten ² – 210 – 2

At this bespeak, nosotros hit a wall. The discriminant of this equation is:

b ² – 4air-conditioning =(-2)² – 4(-1)(-2) = 4 – eight = -4

That's negative, so there are no existent roots for this equation. This means that the function will never cross the x-axis, and so there are no 10-intercepts. This makes sense given that the vertex is at (-i, -2) and the parabola points down, so the function won't go upward towards the x-axis. Approximate nosotros won't need that dynamite afterward all.

Instead of using the x-intercepts, nosotros'll plug in a few extra values of ten and plot those.

We're almost prepare to terminate off this graph. This will be easier to do with a few more points, though. Call back that the axis of symmetry passes through the vertex; we can utilise this to find several more points at present, since we have points on both sides of the vertex.

Compare (0, -4) to the vertex at (-1, -2), for instance. It's 1 to the right on the 10-axis and two lower on the y-axis. Because the function is symmetric, 1 infinite to the left of the vertex will besides be 2 lower on the y-axis, at (-two, -4). Similarly, (-3, -10) is two spaces to the left of the vertex and 8 downwards, and (-4, -xx) is 3 spaces left and 18 spaces downwards. Reflect those onto the right side of the vertex and nosotros'll run across (i, -10) and (2, -20) are as well points on the parabola. Now we can confidently graph this bad boy.

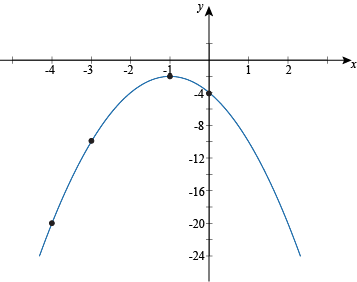
Vertex Parabola Strategery

When you find yourself graphing a parabola in vertex class, here's what y'all do.

Check the sign of a to see if it opens up or down.
Find the vertex and the y-intercept.
Determine if there are any x-intercepts, either by comparing the shape of the parabola and the vertex, or by checking the discriminant of the expanded function.
Observe the ten-intercepts, if they exist.
Bank check if you have enough points to finish the graph. If then, hurray.
If not, boo. Plot a few more points, and use the office'southward symmetry to find more points.
Finish up and call information technology a day.